
第一单元 集合与逻辑 推理与证明
本章知识结构


本章重点难点聚焦
重点:(1)与集合有关的基本概念和集合的“并”、“交”、“补”运算。
(2)全称量词、全称命题、存在量词、特称命题等概念及应用。
(3)充分、必要、充要条件的意义,两个命题充要条件的判断。
(4)合情推理与演绎推理的概念和应用。
(5)直接证明与间接证明的基本方法。
难点:(1)有关集合的各个概念的含义以及这些概念之间的联系。
(2)含有一个量词的命题的否定。
(3)判断充要条件时,区分命题条件和结论。
(4)运用合情推理与演绎推理解决问题。
(5)反证法的证明。
本章学习中注意的问题:
(1)在解答有关集合问题时,首先弄清代表元素,明确元素特点;当集合元素含有参数时,注意元素互异性;在集合运算中注意边界点、临界点及空集可能性。
(2)注意全称命题,特称命题的否定。
(3)研究充分条件,必要条件,充要条件时注意联系命题,注意原命题与逆否命题的等价性。
(4)注意数形结合,分类讨论,等价转化等思想方法的运用。
本章高考分析及预测
(1)近几年来,每年都有考查集合的题目,总体来说这部分试题有如下特点:一是基本题,难度不大;二是大都以选择题、填空题形式出现,有时是解答题的一个步骤。对于集合的考查:一是考查对基本概念的认识和理解,二是对集合知识的应用。无论哪一种形式,都以其他基础知识为载体,如方程(组)、不等式(组)的解集等。
(2)对于逻辑的考查主要考查四种形式的命题和充要条件,特别是充要条件,已经在许多省市的试卷中单独出现,命题形式:一是原命题与逆否命题的等价性(含最简单的反证法);二是充要条件的判定。在考查基础知识的同时,还考查命题转换、推理能力和分析问题的能力以及一些数学思想方法的考查。
(3)推理在高考中虽然很少刻意去考查,但实际上对推理的考查无处不在,从近几年的高考题来看,大部分题目主要考查命题转换、逻辑分析和推理能力,证明是高考中常考的题型之一,对于反证法很少单独命题,但是运用反证法分析问题、进行证题思路的判断经常用到,有独到之处。
(4)预计在2009年的高考中,集合部分的试题还将以选择题或填空题的形式出现,主要考查集合语言与集合思想的运用,考查以集合为背景的应用性、开放性问题,命题将构思巧妙、独特新颖、解法灵活;而对于命题的考查与其它知识相结合,因此基本概念和技能一定要落实好。
§1.1 集合 集合间的基本关系
新课标要求
1、了解集合的含义,元素与集合的“属于关系”。
2、能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题。
3、理解集合之间的包含和相等的含义,能识别给定集合的子集。
4、在具体情景下,了解全集与空集的含义。
重点难点聚焦
重点:(1)集合的概念与表示。
(2)集合之间的基本关系。
难点:(1)集合元素的性质:确定性、互异性、无序性。
(2)元素与集合、集合与集合之间的关系以及符号 的应用。
的应用。
(3)空集的特殊性。
高考分析及预测
集合是数学中最基本的概念之一,集合语言是现代数学的基本语言,因此集合的概念以及集合之间的关系是历年高考的必考内容之一,本部分的考查一般有两种形式:一是考查集合的相关概念,集合之间的关系,题型以选择题、填空题为主;二是考查集合语言、集合思想的理解与应用,这多与其他知识融为一体,题型也是一般以选择填空为主,单纯的集合问题以解答题形式出出现的几率较小,多是与函数、不等式等联系。在复习中还要特别注意,新课标的中特别强调表达与描述同一问题的三种语言“自然语言、图形语言、集合语言”之间的关系,因此要注意利用韦恩图数轴函数图象相结合的作用,另外集合新定义信息题在近几年的命题中时有出现,注意研究。2009年是新课标命题第三年,预测在高考中部分会继续保持稳定难度不会太大,命题形式会更加灵活新颖。
提组设计
再现型题组
1、填空
(1)下列说法中①全中国的大胖子,②小于100的所有质数,③幸福中学高三1班同学,④2008年北京奥运会的所有比赛项目,
以上四个说法不能组成集合的是
(2)集合A= ,则实数k的取值范围是
,则实数k的取值范围是
2、选择
(1)设全集U=R,集合M= ,N=
,N= 则下列关系中正确的是(
)
则下列关系中正确的是(
)
A、M=N B、 C、
C、 D、
D、
(2)给出如下关系式① ②
② ,③
,③ ④
④ ⑤
⑤ ⑥{a}
⑥{a} {a},其中正确的是(
)
{a},其中正确的是(
)
A、①②④⑤ B、②③④⑤ C、②④⑤ D、②④⑤⑥
巩固型题组
3.2008年第29届奥运会在北京召开,现在三个实数的集合,既可以表示为 ,也可以表示为
,也可以表示为 ,则
,则 。
。
4.已知集合 ,则A,B,C之间的关系是
。
,则A,B,C之间的关系是
。
A.  B.
B.  C.
C.  D.
D. 
5.设P,Q为两个非空集合,定义集合 ,若
,若 则
则 中元素的个数是
。
中元素的个数是
。
A. 9 B.
6.记函数 的定义域为A,
的定义域为A,  的定义域为B.
的定义域为B.
(1)求A.
(2)若 ,求实数a的取值范围.
,求实数a的取值范围.
提高型题组
7.已知 ,求实数x.
,求实数x.
8.已知集合 。
。
(1)若 求实数m的取值范围.
求实数m的取值范围.
(2).若 求实数m的取值范围.
求实数m的取值范围.
(3)若 求实数m的取值范围.
求实数m的取值范围.
反馈型题组
9.(08年江西)定义集合运算 ,则集合
,则集合 的所有元素之和为( )。
的所有元素之和为( )。
A . 0 B
10.设集合 ,则正确的是( )
,则正确的是( )

11.(08福建)设集合A= ,B=
,B= ,那么“
,那么“ ”是“
”是“ ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
12.已知集合A= 只有一个元素,则a=
只有一个元素,则a=
13.已知集合 ,集合
,集合 。
。
(1)若 ,求实数a的取值范围;
,求实数a的取值范围;
(2)若 ,求实数a的取值范围;
,求实数a的取值范围;
(3)A、B能否相等?若能,求出a的值;若不能,试说明理由。
14.设A为实数集,满足

 ,
, ,
,
(1)若 ,求A;
,求A;
(2)A能否为单元素集?若能把它求出来,若不能,说明理由;
(3)求证:若 ,则
,则
15.已知集合 ,集合
,集合 ,
,
其中 ,设全集I=R,欲使
,设全集I=R,欲使 ,求实数a的取值范围。
,求实数a的取值范围。
§1.2集合的运算
新课标要求
(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集。
(2)理解在给定集合中的一个子集的补集的含义。会求给定子集的补集。
(3)能使用韦恩图表达集合的关系及运算。
重点难点聚焦
并集、交集、补集的含义,以及两个集合之间并、交、补的运算
高考分析及对策
(1)以考查集合的并、交、补等运算为主,同时注重韦恩,数轴应用,求并、交、补等数形结合的思想的考查。
(2)本节在高考中常以选择、填空题型考查,属容易题。
题组设计
再现型题组
1.已知集合M= 则
则 为
为
A  B
B 
C  D
D

2 已知集合 ,
, ,R是全集。
,R是全集。
①  ②
②  ③
③ ④
④
其中成立的是( )
A ①② B ③④ C ①②③ D ①②③④
巩固形题组
3.设函数 的定义域M,函数
的定义域M,函数 的定义域为N,求
的定义域为N,求
(1)集合M,N
(2)集合 ,
,
4.(08湛江模拟)已知集合 ,N为自然数集合,求
,N为自然数集合,求
5.(07北京)已知集合 ,
, ,若
,若
,求a的取值范围
提高型题租
6.(08广东清远)记函数 的定义域为A,
的定义域为A, ,(a<1)的定义域为B
,(a<1)的定义域为B
(1)求A
(2)若 ,求实数a的取值范围
,求实数a的取值范围
7.已知 ,
, 且
且 求实数m的取值范围
求实数m的取值范围
8.设全集是实数集R, ,
, 。
。
(1)当a=-4时,求
(2)若 ,求实数a的取值范围
,求实数a的取值范围
反馈型题组
9.设全集U是实数集R, ,
, ,则图中阴影部分所表示的集合是(
)
,则图中阴影部分所表示的集合是(
)

A.  B.
B. C.
C.  D.
D.
10.(08广东兴宁模拟)设数集 ,
, ,M、N都是集合
,M、N都是集合 的子集,如果把b-a叫做集合
的子集,如果把b-a叫做集合 的“长度”,那么集合
的“长度”,那么集合 的“长度”的最小值是
的“长度”的最小值是
A.  B.
B.  C.
C.  D.
D. 
11.定义集合A*B= ,设
,设 ,
, 则集合A*B所有元素之和为
则集合A*B所有元素之和为
12.高三某班共有45人,摸底测验数学20人得优,语文15人得优,两门都不得优20人,则两门都得优的人数
13.已知集合 ,
,
(1)若 ,求实数a的取值范围
,求实数a的取值范围
(2)当a取使不等式 恒成立的最小值时,求
恒成立的最小值时,求
§1.3命题、基本逻辑连接词与量词
新课标要求:
1.了解命题及逆命题、否命题与逆否命题
2.了解逻辑连结词“或”“且”“非”的含义。
3.理解全程量词与存在量词的意义。
4.能正确地对含有一个量词的命题进行否定。
5.学会运用等价转化思想进行推理。
重点难点聚焦:
本节内容的重点是有关命题的概念及四种命题间的相互关系;逻辑联结词的含义及命题真假的判定;全称量词与存在量词的有关概念。
本节内容的难点:是对含有一个量词的命题的否定,含有逻辑联结词的命题的真假的判断,以上是重点突破的内容。
高考分析及预测:
1.考查命题转化,逻辑推理能力和分析问题,解决问题的能力。多以选择题、填空题的形式出现。
2.全称量词与存在量词作为新增内容,很有可能在选择题,填空中出现。
题组设计
再现型题组:
1. 分别指出由下列命题构成的“ ”,“
”,“
 ”“
”“ ”形式的命题的真假。
”形式的命题的真假。
(1)p:  , q:
, q: 
(2)p:1是奇数,q:1是质数
(3)p:  q:
q: 
(4)p:  q:27不是质数
q:27不是质数
(5)p:不等式 的解集是
的解集是
q:不等式 的解集是
的解集是
2. 写出下列命题的否定,并判断命题的否定的真假,指出命题的否定属于全称命题还是特称命题:
(1)所有的有理数是实数。
(2)有的三角形是直角三角形
(3)每个二次函数的图像都与Y轴相交
(4)
巩固型题组
3. 如果命题“ ”是真命题,命题“
”是真命题,命题“  ”是假命题,那么()
”是假命题,那么()
(A)命题p和命题q都是假命题
(B) 命题p和命题q都是真命题
(C) 命题p和命题非q真值不同
(D) 命题p和命题非q真值相同
4.已知 ,设命题p:函数
,设命题p:函数 在R上单调递增;命题q:不等式
在R上单调递增;命题q:不等式 对
对 恒成立,若p且q为假,p或q为真,求a的取值范围。
恒成立,若p且q为假,p或q为真,求a的取值范围。
提高型题组
5设P:关于x的不等式 的解集是
的解集是 ,Q:函数
,Q:函数 的定义域为R,如果P和Q有且仅有一个正确,求a的取值范围.
的定义域为R,如果P和Q有且仅有一个正确,求a的取值范围.
6(2007年江苏统考)下列命题中不正确的是()
A.  ,有
,有 是等差数列
是等差数列
B. 
 ,使
,使 是等差数列
是等差数列
C. 
 ,有
,有 是等差数列
是等差数列
D. 
 ,使
,使 是等差数列
是等差数列
反馈型题组:
7. 已知命题p:  ,
, 则( )
则( )
A.  :
:  B.
B.  :
:
C.  :
:  D.
D.  :
:
8. 命题“存在 ,使
,使 ”的否命题是()
”的否命题是()
A.存在 ,使
,使 >0
>0
B. 不存在 ,使
,使 >0
>0
C.对于任意 都有
都有
D. 对于任意 都有
都有 >0
>0
9. 命题“若ab=0,则a=0或b=
A.若 ,则
,则 或
或
B. 若 或
或 ,则
,则
C. 若 ,则
,则 且
且
D. 若 且
且 ,则
,则
10. 命题p:不等式 的解集为
的解集为 ,命题q:“A=B”是“sinA=sinB”成立的必要非充分条件,则( )
,命题q:“A=B”是“sinA=sinB”成立的必要非充分条件,则( )
A.p真q假 B.“p且q”为真
C. “p或q”为假 D.p假q真
11. 与命题
“若 ,则
,则 ”等价的命题是()
”等价的命题是()
A. 若 ,则
,则 B. 若
B. 若 ,则
,则
C若 则
则 D. 若
D. 若 则
则
12. 如果命题“ ”为假命题,则(
)
”为假命题,则(
)
A.p、q.均为真命题
B. p、q.均为假题
C..p、q.中至少有一个为真命题
D .p、q.中至多有一个为真命题
13. 已知命题p:  ,q:
,q:  ,且 “p且q”与“非p”同时为假命题,求x的值。
,且 “p且q”与“非p”同时为假命题,求x的值。
§1.4充分条件,必要条件与四种命题
新课标要求
1.本节涉及到的主要基础知识
(1)了解命题及其逆命题,否命题,逆否命题
(2)理解充分条件,必要条件与充要条件的意义,会分析四种命题的相互关系
2.常用的数学思想方法
演绎法,特例法,转化思想法
3.主要能力
运算能力和逻辑思维能力
重点难点聚焦
本节重点难点是四种命题的等价转化和充分条件,必要条件,充要条件的判断
高考分析和预测
近几年的高考命题中,命题成立的充分,必要及充要条件的求解和判断问题;四种命题的关系已成为高考命题的首选素材。一方面这类问题具有很深广的开放性,另一方面命题的空间广阔,可与多个知识点进行交汇,命题素材随处可见。
题组设计
再现型题组
1.分别写出下列命题的逆命题、否命题、逆否命题,并判断它们的真假。
(1)若 ,则方程
,则方程 有实根;
有实根;
(2)若 ,则
,则 或
或 ;
;
(3)若 ,则
,则 全为零
全为零
2.在下列各题中,判断A是B的什么条件,并说明理由
(1)A:  方程
方程 有实根;
有实根;
(2)A:圆 与直线
与直线 相切,B:
相切,B:
巩固型题组
3.已知 :
: ,且
,且 是
是 的必要而不充分条件,求实数m的取值范围。
的必要而不充分条件,求实数m的取值范围。
4.下列命题:(1)“若xy=0则x,y中至少有一个为零”的否命题(2)
面积不相等的三角形不全等,(3)“若 ,则
,则 有实根”的逆否命题,(4)
有实根”的逆否命题,(4) 是方程
是方程 表示直线的充分不必要条件,其中真命题有
表示直线的充分不必要条件,其中真命题有
提高型题组
5.分别写出下列命题的逆命题,否命题,逆否命题,命题的否定,并判断它们的真假:
(1)若 ,则方程
,则方程 有实根;
有实根;
(2)若 都是奇数,则
都是奇数,则 是偶数;
是偶数;
(3)若 ,则
,则 或
或 ;
;
(4)若 ,则
,则 全为0.
全为0.
6.已知抛物线C:  和点A(3,0),B(0,3).求证:抛物线C与线段AB有两个不同的交点的充要条件是
和点A(3,0),B(0,3).求证:抛物线C与线段AB有两个不同的交点的充要条件是
反馈型题组
7(2007重庆)命题“若 ,则
,则 ”的逆否命题是(
)
”的逆否命题是(
)
A.若 ,则
,则 ,或
,或 B.若
B.若 ,则
,则
C.若 ,或
,或 ,则
,则 D.若
D.若
三、解答题
11、证明:假设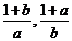 都不少于2,则
都不少于2,则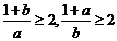
因为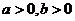 ,所以
,所以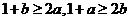 ,
,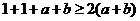
即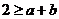 ,这与已知
,这与已知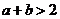
相矛盾,故假设不成立
综上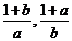 中有一个小于2
中有一个小于2
12、解:P: 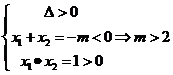
Q: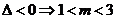
(1)若P假Q真,则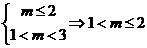
(2)若P真Q假,则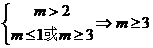
所以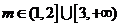
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com